| MISHLOVE: It’s a pleasure to have you here. You know, many academic psychologists — and perhaps you have some sympathy for this point of view — over the years have taken a perspective which laymen tend to laugh at, at times. They claim that the mind doesn’t exist. I wonder if you can explain that perspective — talk about what we mean, or what you mean, by the mind.
PRIBRAM: Well, I don’t like the term the mind, because it reifies — that means it makes a thing of — something that’s a process. We pay attention, we see, we hear. Those are all mental processes, mental activities. But there isn’t a thing called the mind. There might be something you want to call yourself, but the mind sort of makes something concrete out of something that’s very multifaceted.
MISHLOVE: Yet somehow when I’m aware of myself being aware, I think, “Well, that’s my mind that does that.”
PRIBRAM: That does that; that your mind does it. I’d have to think about that.
MISHLOVE: You’re very well known in psychology and in neuropsychology as the developer of the holographic or holonomic model of the brain. Can you talk about that a little bit, and how it relates to the mind — or rather, to the mind-body process? I have to be on my toes with you today.
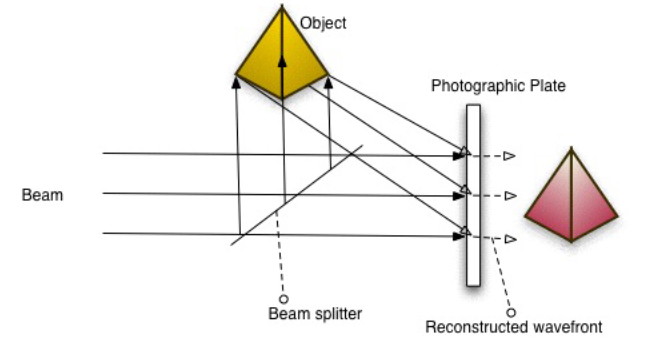
PRIBRAM: Yes. The holonomic brain theory is based on some insights that Dennis Gabor had. He was the inventor of the hologram, and he obtained the Nobel Prize for his many contributions. He was a mathematician, and what he was trying to do was develop a better way of making electron micrographs, improve the resolution of the micrographs. And so for electron microscopy he suggested that instead of making a photograph — essentially, with electron microscopes we make photographs using electrons instead of photons. He thought maybe instead of making ordinary photographs, that what he would do is get the interference patterns. Now what is an interference pattern? When light strikes, or when electrons strike any object, they scatter. But the scatter is a funny kind of scatter. It’s a very well regulated scatter. For instance, if you defocus the lens on a camera so that you don’t get the image falling on the image plane and you have a blur, that blur essentially is a hologram, because all you have to do is refocus it.
MISHLOVE: Contained in the blur is the actual image.
PRIBRAM: That’s right. But you don’t see it as such. So one of the main principles of holonomic brain theory, which gets us into quantum mechanics also, is that there is a relationship here between what we ordinarily experience, and some other process or some other order, which David Bohm calls the implicate, or enfolded, order, in which things are all distributed or spread — in fact the mathematical formulations are often called spread functions — that spread this out.
MISHLOVE: Now what you’re talking about here is the deep structure of the universe, in a way. Beneath the subatomic level of matter itself are these quantum wave functions, so to speak, and they form interference patterns. Would I be wrong in saying it would be like dropping two stones in a pond, the way the ripples overlap? Is that like an interference pattern?
PRIBRAM: That’s certainly the way interference patterns work, yes.
MISHLOVE: And you’re suggesting that at that very deep level of reality, something is operating in the brain itself.
PRIBRAM: Well, no. In a way, that’s possible, but that’s not where the situation is at the moment. All we know is that the mathematical descriptions that we make of, let’s say, single-cell processes, and the branches from the single cells, and how they interact with each other — not only anatomically, but actually functional interactions — that when we map those, we get a description that is very similar to the description of quantum events.
MISHLOVE: When you take into account that there are billions of these single cells operating in the brain.
PRIBRAM: That’s right. And the connections between them, so there are even more; there are trillions of connections between them. They operate on the basic principles that have been found to also operate at the quantum level. Actually, it was the other way around. The mathematics that Gabor used, he borrowed from Heisenberg and Hilbert. Hilbert developed them first in mathematics, and then Heisenberg used them in quantum mechanics, and Gabor used them in psychophysics, and we’ve used it in modeling how brain networks work.
MISHLOVE: So in other words, in the brain,when we look at the electrical impulses traveling through the neurons, and the patterns as these billions of neurons interact, you would say that that is analogous, I suppose, or isomorphic to the processes that are going on at the deeper quantum level.
PRIBRAM: Yes. But we don’t know that it’s a deeper quantum level in the brain.
MISHLOVE: That may or may not be the case.
PRIBRAM: Analogous isn’t quite the right word; they obey the same rules. It’s not just an analogy, because the work that described these came independently. An analogy would be that you take the quantum ideas, and see how they fit to the data we have on the brain. That’s not the way it happened. We got the brain data first, and then we see, look, it fits the same mathematics. So the people who were gathering these data, including myself, weren’t out to look for an analogous process. I think it’s a very important point, because otherwise you could be biased, and there are lots of different models that fit how the brain works. But this is more based on how the brain was found to work, independent of these conceptions.
MISHLOVE: Independent of any model.
PRIBRAM: Yes, essentially independent of any model.
MISHLOVE: So you’ve got a mathematical structure that parallels the mathematical structures of quantum physics. Now what does that tell us about the mind?
PRIBRAM: What it tells me is that the problems that have been faced in quantum mechanics for the whole century — well, since the twenties —
MISHLOVE: Many paradoxes.
PRIBRAM: And very many paradoxes — that those paradoxes also apply at the psychophysical level and at the neuronal level, and therefore we have to face the same sets of problems. At the same time, I think what David Bohm is doing is showing that some of the classical conceptions which were thought not to apply at the quantum level, really do apply at the quantum level. Now, I’m interpreting Bohm; I’m not sure he would want to agree to my interpretation of what he’s doing. But to me that seems to be what is going on. So that the schism between levels — between the quantum level, the submicroscopic almost, subatomic level and what goes on there, and the classical, so-called uncertainty principle and all of that — that all applies all the way along; but you’ve got to be very careful in — how should I put it? You’ve got to apply it to the actual data, and not just sort of run it over.
MISHLOVE: To the average layman, why would they be interested in this? Is there some significance to people in their everyday lives, or in their workaday worlds, in the business of life?
PRIBRAM: Sure, and this is the critical thing — that if indeed we’re right that these quantum-like phenomena, or the rules of quantum mechanics, apply all the way through to our psychological processes, to what’s going on in the nervous system — then we have an explanation perhaps, certainly we have a parallel, to the kind of experiences that people have called spiritual experiences. Because the descriptions you get with spiritual experiences seem to parallel the descriptions of quantum physics. That’s why Fritjof Capra wrote The Tao of Physics, why we have The Dancing Wu Li Masters, and all of this sort of thing that’s come along. And in fact Bohr and Heisenberg already knew; Schroedinger talked about the Upanishads, and Bohr used the yin and yang as his symbol. Because the conceptions that grew out of watching the quantum level — and therefore now the neurological and psychophysical level, now that it’s a psychological level as well — seem to have a great deal in common with our spiritual experience. Now what do I mean by spiritual experience? You talked about mental activity, calling it the mind. That aspect of mental activity, which is very human — it may be true of other species as well, but we don’t know — but in human endeavor many of us at least seem to need to get in contact with larger issues, whether they’re cosmology, or some kind of biological larger issue, or a social one, or it’s formalized in some kind of religious activity. But we want to belong. And that is what I define as the spiritual aspects of man’s nature.
MISHLOVE: Some sense of relationship to the larger cosmos, to the world about us.
PRIBRAM: And that part has this implicate order. It has the explicate order, too — you know, the ordinary space-time order.
MISHLOVE: I want to stop for a second, because you’re using Bohm’s term implicate order, and we haven’t really quite defined that.
PRIBRAM: It’s the holographic. You described it very well, with the pebbles. It’s a set of relationships which —
MISHLOVE: It’s a fuzzy picture.
PRIBRAM: Well, yes, and you can talk about it in terms of waves, or you can talk about it in terms of mathematical matrices which have vectors in them, and so on. You can have continuous vectors, or you can have continuous matrices. You can have all kinds of relationships between. When you look at a photographic plate that has a hologram on it, you can either look at some of the swirls in there, or you can look at the individual grains of silver. So there are lots of kinds of mathematics, but they all fit together, whether it be Schroedinger’s equation, which is a wave equation, or Heisenberg’s more matrix kind. These are not relevant to the ordinary person, but I just want to say it here, because otherwise we get stuck in the wave, as if it were all waves, and that’s too simple.
MISHLOVE: But what you’re saying, if I can try and simplify it, is that there’s a level of reality at which things are what they appear to be. I look at you and I see a body and a face. That would be the explicate level, where things are what they appear to be. Then there’s an implicate level, which is just as real, but if you were to look at it, it doesn’t look at all like the other.
PRIBRAM: We experience it entirely differently — as a spiritual aspect of our being. This implicate order is also a potential order; we’re not in it most of the time. We had for years this whole idea of the human potential, and I think that’s what we’re talking about.
MISHLOVE: Human potential may be embodied somehow in the implicate structure.
PRIBRAM: That’s very nice, yes. Good way to say it.
MISHLOVE: Prior to the development of quantum physics and the holonomic model of the brain, people based their notion of who they were and how their minds worked more on the Newtonian classical models of physics, and perhaps in some sense, if they bought into those models, would tend to deny their spiritual experiences, or not really feel connected with that part of themselves. Would you say so?
PRIBRAM: Very definitely, and that recalls something that De Tocqueville said. After writing his histories, he said, “Maybe I’ve been interpreting it the wrong way, because I’ve been doing it in terms of classical mechanics, with cause-and-effect relationships. But when the human being acts, this is not a cause; this is a challenge.”
MISHLOVE: He wrote the books on capitalism and democracy.
PRIBRAM: Democracy in America, and all. When we act it’s a challenge, and that’s very much a quantum-type, holographic, implicate-order type idea. Rather than having causality —
MISHLOVE: It’s moving towards a goal.
PRIBRAM: No, it isn’t. It’s a challenge, it’s different. Moving toward a goal would still be causal. See, we don’t even have a good language to talk about all this. It’s a challenge. The whole system can reorganize on the basis of this challenge, and you never find out where the cause is. When we were talking earlier, you said, “Where does the will start?” Well, it’s a challenge. The whole system does it. There isn’t a start and a midst and so on, because time and space are enfolded, and therefore there’s no causality.
MISHLOVE: It’s all just emerging.
PRIBRAM: It’s emerging, and you can challenge the system, and it will respond in an unpredictable way.
MISHLOVE: You know, I must say I’m a little bit surprised, because you described yourself earlier to me as a positivist of sorts, and a behaviorist, and in a way the language that you’re using seems very much like the language of the Buddhists, who talk about no self, and just process.
PRIBRAM: No thing. One of the chapters I wrote once was “The Non-sense of No-thing,” –– the nonsense of nothing. But it’s nonsensory, because senses are lenses, and as David Bohm has said so well, if you take the lenses away you’ve got a hologram. Lenses tend to reify, to objectify and articulate particles. Take the lenses away and you’ve got this distributed.
MISHLOVE: So part of our mind-brain process functions as a lens, then.
PRIBRAM: Well, certainly the senses do, right.
MISHLOVE: What about the other functions of the mind — memory, learning?
PRIBRAM: The what?
MISHLOVE: You caught me again. It’s such a habit.
PRIBRAM: Other mental functions. It’s easy to say it without reifying it, especially if you want to be holistic about this. In answer to your previous question — just a second if I may interrupt — you said I’m a positivist. You know, the hard-nosed kind of scientist, in my experience, which was the stimulus-response scientists, became very soft after awhile. That was the hardest, hard-nosed kind of science, and the cognitive, which was soft, became the hard-nosed one. And I’m quite sure that the kind of definitions I’m giving are just as hard as anything that ever was in stimulus-response psychology.
MISHLOVE: In other words, at some point it will come to be seen that if you talk about spiritual experiences — if you refer to Buddhists and mystical concepts — that can be taken in terms of very hard core.
PRIBRAM: Well, it’s up to scientists to do this. It doesn’t come automatically.
MISHLOVE: Very rigorous.
PRIBRAM: Well, you don’t want to get into rigor mortis, but yes. You see, the beauty of science is that it’s basically based on sharing. Now, the more carefully and clearly I can define something — and the reason we want to quantify is not because we’re interested in quantities, but because then you can communicate and share much more clearly than if you can’t have quantities. So all of science is based on the notion of sharing, and we need to define things. If some Buddhist tells me, “I’ve just had a high experience,” or “I’ve just seen the light,” and I don’t know what the hell he’s talking about, then I can’t share that. But if he gets me to have the same experience, that begins to be science. And if I can make definitions so I can describe to you what is going on — let’s say the pineal is secreting some substance that makes you suddenly flash, or something of that kind — then we have some way of sharing this experience, which goes deeper than when we’re sort of just stunned by somebody saying, “Yes, I’ve seen the light.” I mean, that may be just metaphorical, or it may actually be that they did produce a reaction akin to stimulation of the visual system. And so on and so forth.
MISHLOVE: You’re raising many issues here. I don’t want to get too off track, though.
PRIBRAM: Well, my point is simply that this business of what’s soft and what’s hard keeps changing.
MISHLOVE: That’s a very important point.
PRIBRAM: My prediction is that the kind of thing we’re dealing with here will be seen as as solid and as scientific. In the twenty-first century we’ll look back at some of the fuzzy stuff that was done in the name of behaviorism.
MISHLOVE: Many neuroscientists today — it’s almost axiomatic, when they talk about the mind, which they sometimes do — they say the mind is sort of located in the brain. I gather that that way of putting it is totally discordant with your own view of things.
PRIBRAM: Yes. There are lots of different ways of phrasing this. One is that mental phenomena are emergent properties of how the brain works, and so it’s almost like the brain is secreting vision and mind and all that. But maybe a better way of talking about it would be to say that mental phenomena arise through the interaction between brain and body and the environment and — this is what Karl Popper says — that whole interactive thing produces an emergent, which we call mind and spirit, and so on. I think that’s a better way than just thinking of the brain secreting it.
MISHLOVE: Now how does this model relate to human potential? If I want to cultivate my various potentialities, my skills, reach into the implicate order and make some of it more explicate, do you have notions about that, for learning, for human development?
PRIBRAM: Well, you said it yourself just now. You reach into the implicate order. You allow yourself — Freud called it regression in the service of the ego, primary process kinds of things, which are more holonomic, more holographic-like. Yes, I think that’s the general way that I would say that this is different. The other is imitation, and the kind of thing where we have role models and we take care of ourselves, model ourselves on someone — the kind of thing you do in sports, you watch a videotape or something.
MISHLOVE: Would you say creativity works the same way?
PRIBRAM: Well, creativity works the same way in the following sense: that we allow ourselves to get — let’s just be very crude here — into this wave form, you know, in a distributed system. And this then allows the fluctuations that take place there to create new forms, which in space-time we can’t really do too well. I mean, things are already formed. But if we get back into this potential, of distributed, implicate-type order, then these fluctuations have a chance to reorganize this way, or to organize new foci of activity.
MISHLOVE: And these would take the shape of mental images in our mind?
PRIBRAM: By the time they get to be mental images, it’s already pretty well set into space-time form.
MISHLOVE: What is a mental image, in space-time? How would you describe that, as a neuroscientist?
PRIBRAM: Well, let’s see. I’ve got my image of your face right now, and I also have an image of a person sitting in a chair over there, and a big eye looking at me in front, a television eye, with my eyes closed. That’s mental imagery.
MISHLOVE: You wouldn’t try and tie that to resonant neural patterns?
PRIBRAM: Oh sure, I’ll be happy to do that. There are two kinds of mechanism — I mean, you can sort of divide things up into twos and threes and so on. But if you divide neural activity, you can divide it into propagative nerve impulses on the one hand, and then these slow potentials — hyperpolarizations, steep polarizations — that don’t go anywhere. And they form this holographic-like pattern, and it’s those that I feel — and I have some evidence to support this — are what we experience as images.
MISHLOVE: Would these sort of be like standing waves in the mind? Am I reaching too far here?
PRIBRAM: You said it — “in the mind” — again. The waves aren’t in the mind.
MISHLOVE: Standing waves in the brain.
PRIBRAM: In the brain. They could be thought of that way. Again, I use the matrix analogy as well, just so we don’t get too far into the waves. But sure, some kind of standing wave forms that are there temporarily. Sometimes they last longer, and sometimes they are very brief and we are not even aware of them. But the longer they last — Sherrington had this idea, and he said there seems to be a reciprocal relationship between reflex and mind; the more reflex the less mental, and vice versa.
MISHLOVE: OK. That relates somehow to free will also, I gather.
PRIBRAM: Well, there we get into a different set of problems, now. Sure, to some extent if you get into your potential mode, then new things can happen. But usually free will is conceived of in terms of how many constraints are operating, and we have in statistics a notion of degrees of freedom. I think our will essentially is constrained, more or less. We have so many degrees of freedom, and the more degrees of freedom we have, the more we feel free, and we have freedom of choice.
MISHLOVE: What can we say, in wrapping the program up, given all these aspects of the mind-brain system that you’ve described, how does that relate to, say, the ultimate or the farther reaches of human potential?
PRIBRAM: Well, I think in the twenty-first century we’re going to be able to do an awful lot that we weren’t able to do up to now, simply because science will be admitted to the spiritual aspects of mankind, and vice versa — what has been segregated for at least three hundred years, since Galileo, where the spiritual aspects, in Western culture at least, have been sort of relegated over here. People have split this, you know. We build buildings, and we do surgery, and do all of these things. Then we have a spiritual aspect to ourselves; we go do that somewhere else. Whereas now I think these things will come together, and it will be perfectly all right for what we today call “faith healers” to come and help with reduction of pain and to ease all kinds of things. So it’ll be a different world. I wouldn’t even be surprised if preventative therapies could be instituted, that deal with controls of ourselves, so we aren’t as prone to get cancers and so on.
MISHLOVE: That’s very optimistic. Well, Karl Pribram, it’s been a pleasure having you with me. Thank you very much.
|