Quantum Transform’s Bimodal Distribution is analogous to the Schrodinger equation and is equal to the complex sum of the energy’s and order’s logarithmic distributions, where RLognormal[(Δf)h] is the real part and RLognormal(O) is the imaginary part.
Written below we get the eqation for the Quantum Information Field Energy randomness observed at the multibifurcation point of the spacetime:
\hat {H}[B]|\Psi (t)\rangle => RLognormal[(\Delta f) h]+ j \frac{\varphi(t)}{RLognormal(O)}
4π Δf Δt = 1
4π Δf Δt > 1
Heisenberg uncertainty: frequency version which describes transition between the Minkowski space to tachyon space, where Δf is the frequency uncertainty and Δt is time uncertainty.
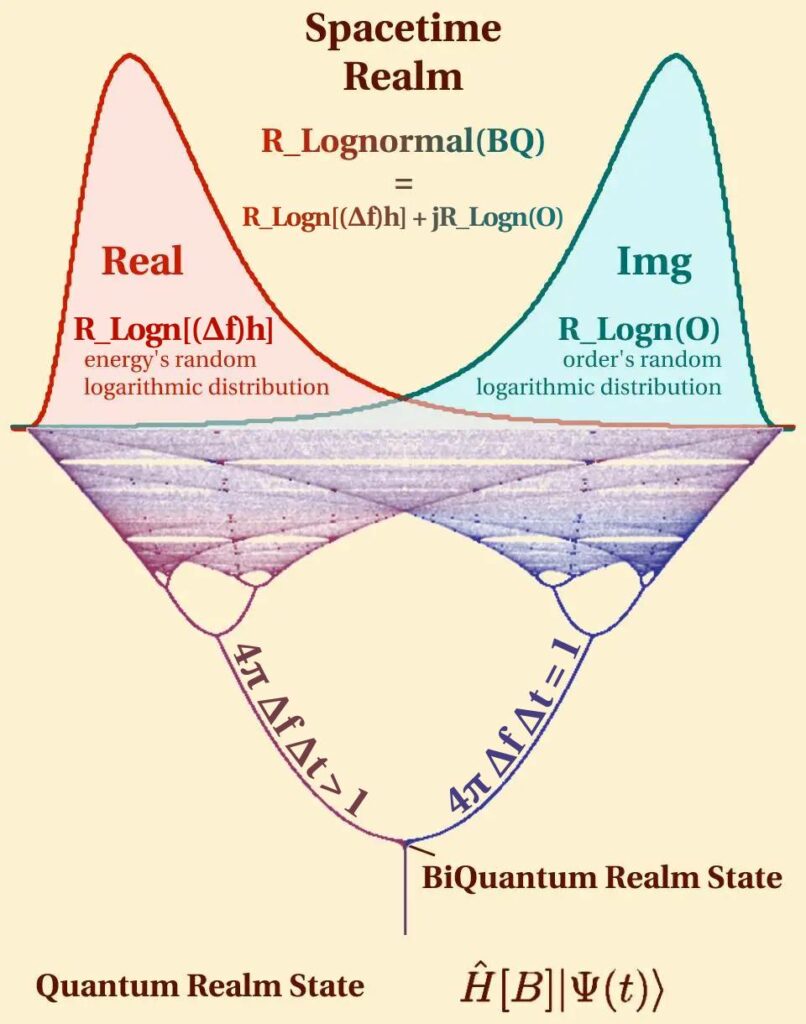
Bifurcation with asymmetry emerges from the Quantum Energy randomness with BiQuantum Realm State, where Quantum Transform’s Bimodal Distribution is equal to the complex sum, the real part RLognormal[(Δf)h] is random logarighmic distribution representing changes in system’s frequency uncertainty, while the imaginary part RLognormal(O) is order’s random logarighmic distribution. 4π Δf Δt = 1 and 4π Δf Δt > 1 describe transition between the Minkowski space to tachyon space, where Δf is the frequency uncertainty and Δt is time uncertainty [3].