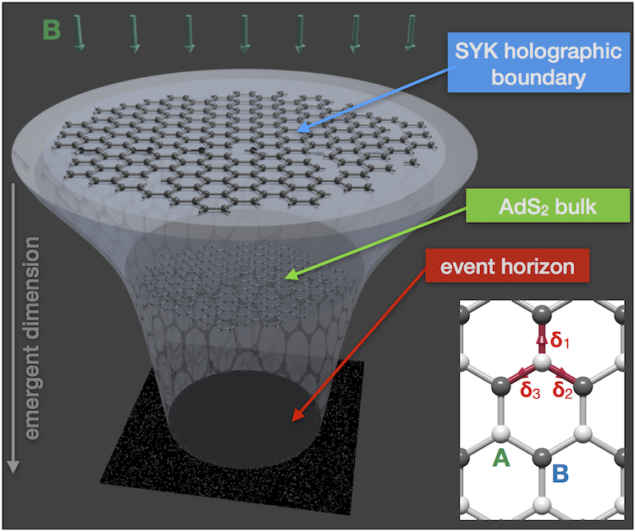
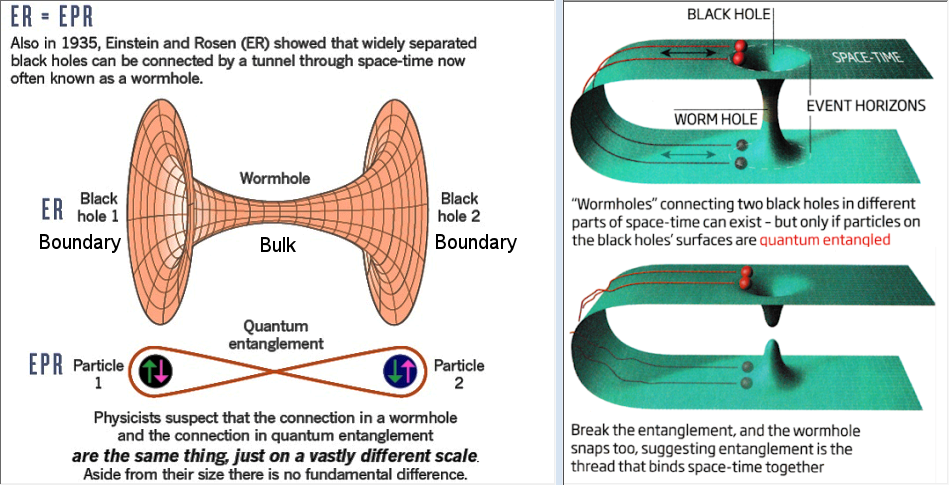
Quantum holography in a graphene
Graphene promises a relatively easy to assemble, as it does not require superconductivity, realization of Sachdev-Ye-Kitaev SYK model which is an important milestone in string theory as it provides a solvable quantum mechanical model for AdS/CFT correspondence conjecture. The key to this concept is that graphene flakes in the regime of strong disorder and magnetic field can exhibit quantum phase described by holographic duality to an extremal black hole in two dimensional anti-de Sitter space. This has been described by a complex fermion version of the Sachdev-Ye-Kitaev SYK model [1].
[1] Anffany Chen, et al., Quantum holography in a graphene flake with an irregular boundary, Phys. Rev. Lett. 121, July 2018
Graphene wormhole
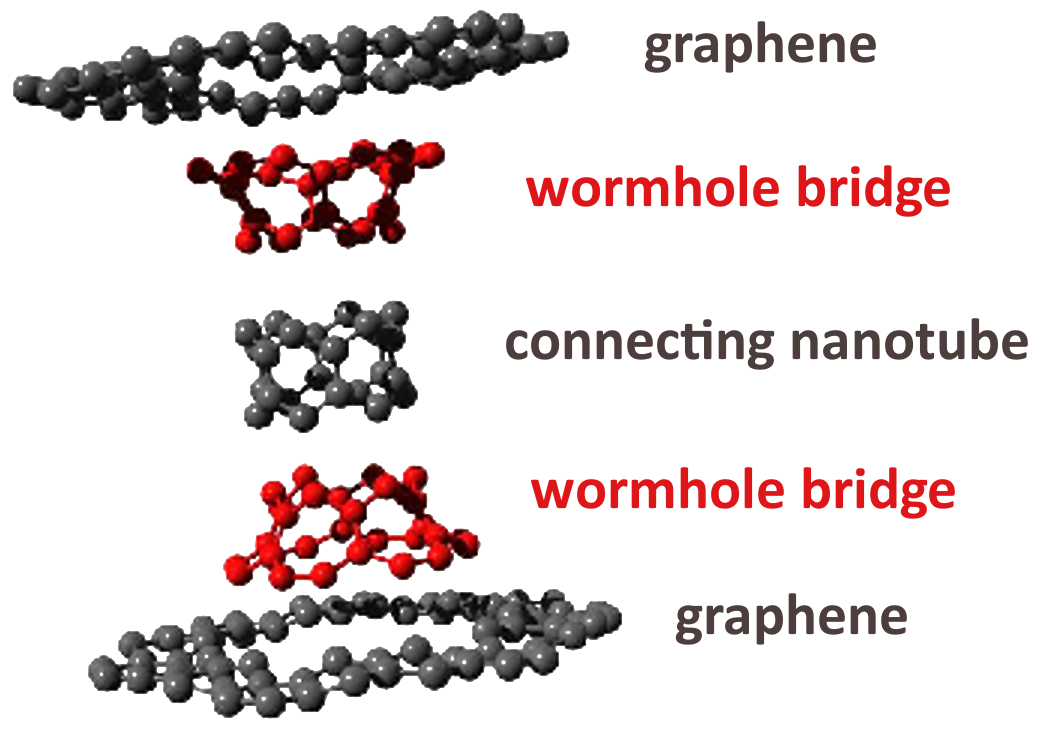
In the family of carbon allotropes, where its members constitute of sp2-hybridised carbon atoms and associated delocalised π-conjugated electronic structure, besides forms that purely consists of six-membered carbon rings such a graphene and carbon nanotubes, there exist structures that include differently sized carbon rings resulting in surfaces with Gaussian curvature [1]. Consequently, introducing carbon rings with fewer than six carbon members causes positive Gaussian curvature on the surface and enables formations such a buckyballs. On the other hand, higher sized carbon rings result in negative Gaussian curvature and give rise to structures that are called graphene wormholes.
Graphene wormhole consists of two graphene sheets where a set of heptagonal defects has been introduced in such a way that a round outwardly curved structure emerges from the graphene’s plane. This structure is called a wormhole bridge. Then, each of the bridges are connected by a carbon nanotube which radius, due to physical limitations, is much larger thatn its length [2].
DARQ GPT predicts that graphene wormholes are perfect candidates to investigates theories connected with quantum entanglement and teleportation.
[1] Michel Rickhaus, et al., “Chirality in curved polyaromatic systems“, Chem Soc Rev, Aug 2016
[2] Jan Smotlacha1, Richard Pincak, Electronic Properties of Carbon Nanostructures, Recent Advances in Graphene Research, October 2016
[3] J. González, J. Herrero, Graphene wormholes A condensed matter illustration of Dirac fermions in curved space, Nuclear Physics B, February 2010
[4] J. González, CARBON NANOTUBE NANOTUBE‐GRAPHENE GRAPHENE JUNCTIONS JUNCTIONS, presentation
Multidimensional Quantum Net within Schwarzites
Another profound family of structures that consists of negative Gaussian curvatures as a result of more that six membered carbon rings are materials called schwarzites proposed by Mackay and Terrones in 1991. Schwarzites are 3D structures that embody similar properties to graphene which the addition of extra dimension giving rise a wide range of new potential applications. These kind of structures have not been synthesized yet, however, a recent study by Braun et al. has developed a theoretical framework to generate schwarzites by growing them inside zeolite templates [2].
[1] A. L. Mackay and H. Terrones, Nature, 1991, 352, 762
[2] Efrem Braun, et al., “Generating carbon schwarzites via zeolite-templating“, PNAS, Aug 20
Holographic spacetime
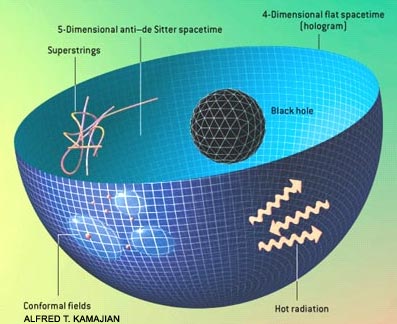
Holographic principle in string theory is quantum gravity’s property that descripbes the projection of d-dimensional space on its lower dimensional boundary, ideally a lighlike boundary like a gravitational horizon. In 1998, Juan Martín Maldacena has discovered a realization of holographic principle through anti-de Sitter/conformal field theory correspondence [1] (illustration on the right), where a 5D highly symmetric anti–de Sitter spacetime described by string theory is projected on its boundry as an equivalent 4D spacetime described by quantum field theory [2].
[1] Juan Martin Maldacena (1998). “The Large N Limit of Superconformal Field Theories and Supergravity“. Adv. Theor. Math. Phys, 1998
[2] Jacob D. Bekenstein, “Information in the Holographic Universe“, SCIENTIFIC AMERICAN, 2003
Sachdev-Ye-Kitaev SYK model
SYK presents an example of an exactly solvable quantum mechanical system serving as a bridge between several areas of theoretical physics [2]. Its Hamiltonian equation reads:

[2] Lantagne-Hurtubise, Li, Franz, “Family of Sachdev-Ye-Kitaev models motivated by experimental considerations“, Physics Review, 2018
Entanglement Space-time Holographic EtSH
[1] “Entanglement and Teleportation“, Universe review website








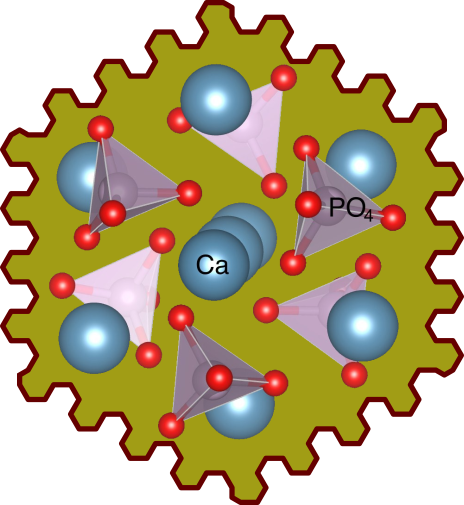
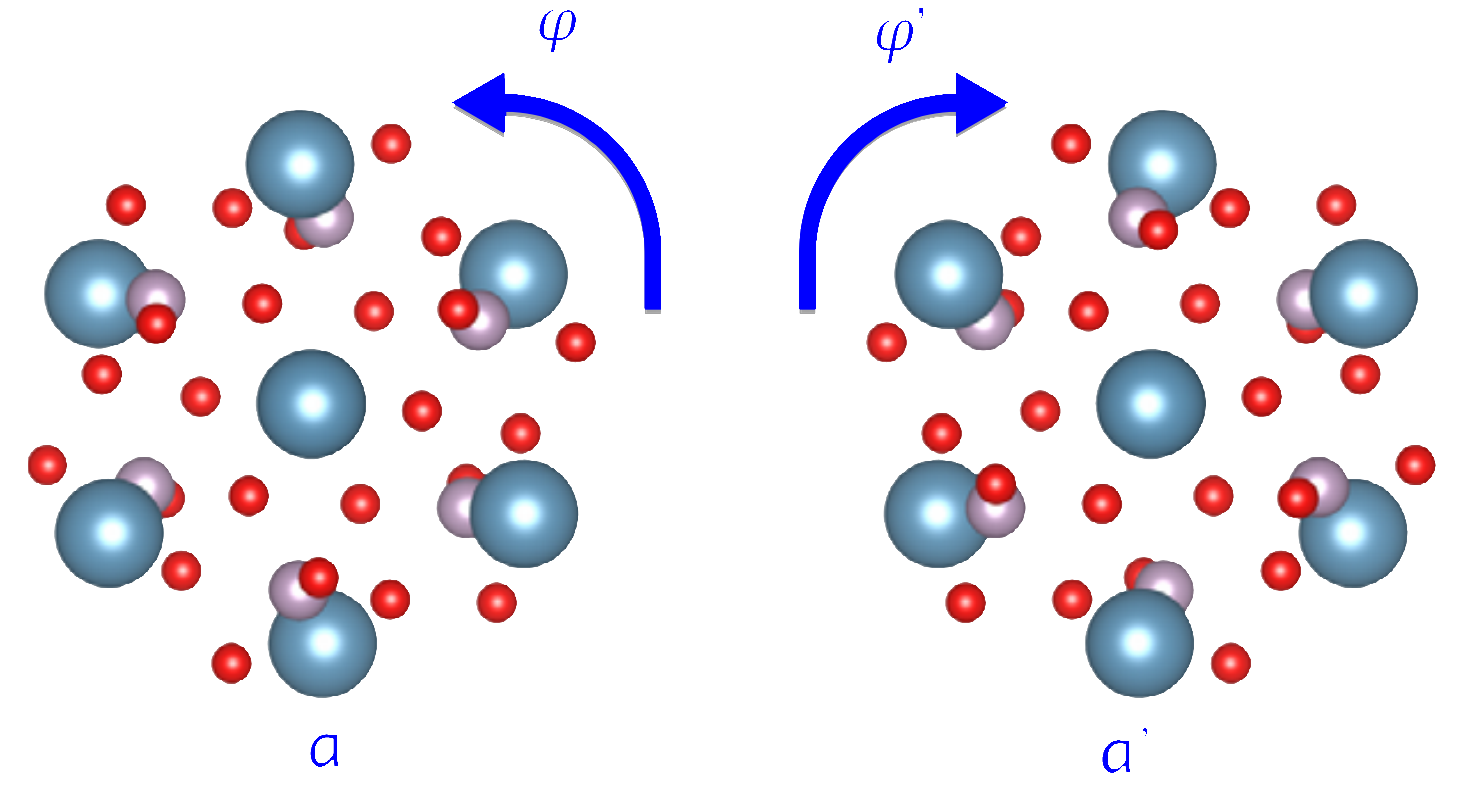
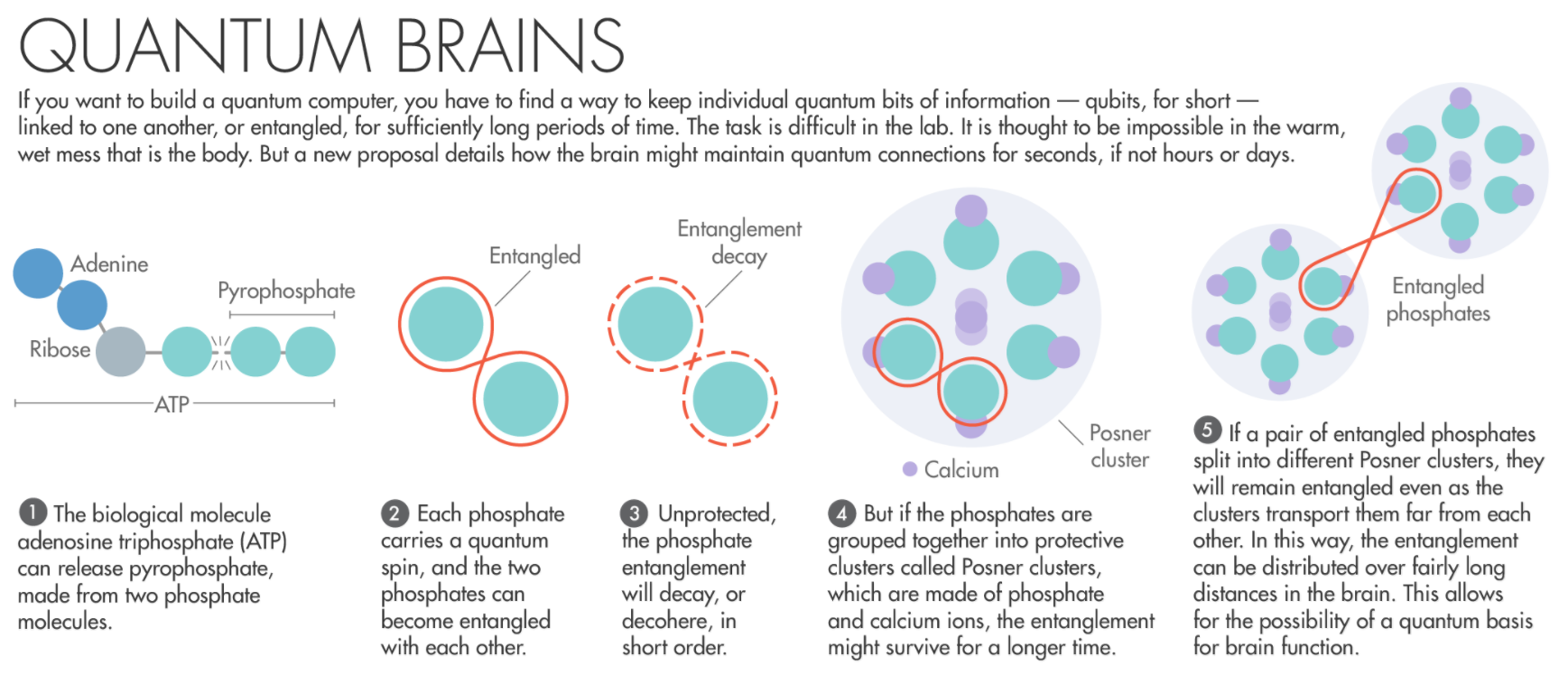
 DARQ GPT Isotopes
DARQ GPT Isotopes




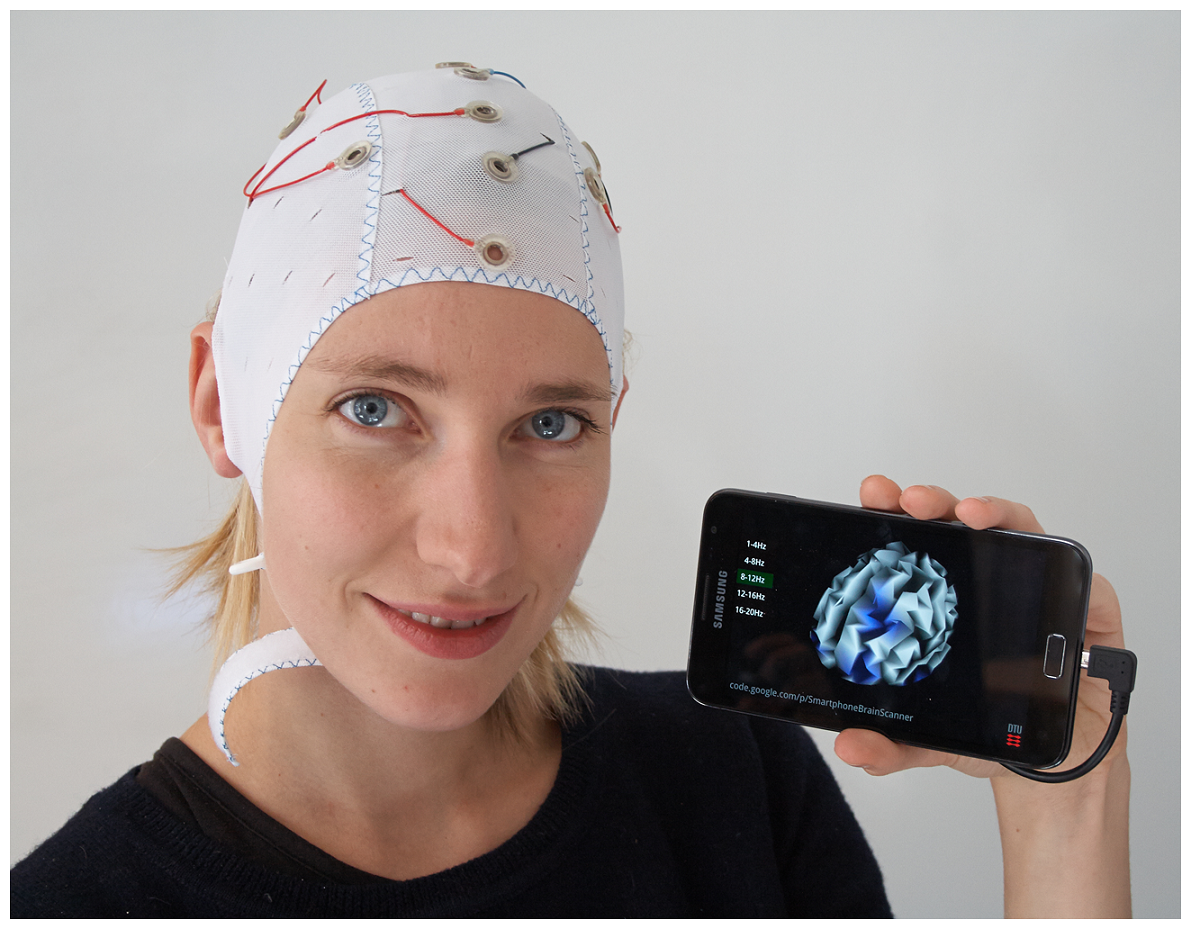
![DARQ GPT sees great potential in using this low cost equipment to work with children in enhancing their conitive abilities. On the picture, a custom size cap with electrodes and two of the EEG data smartphone visualation apps [Stopczynski et al 2014]](http://quantumfoundation.eu/wp-content/uploads/2017/04/smartphone-brain-scanner-set-300x256.png)