Quantum Holo News

Posted on

Quantum~Holographic Informational Consciousness

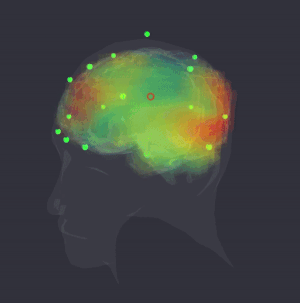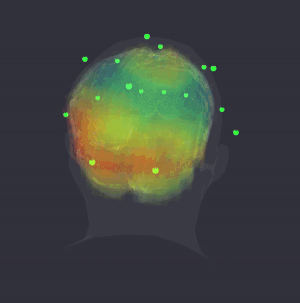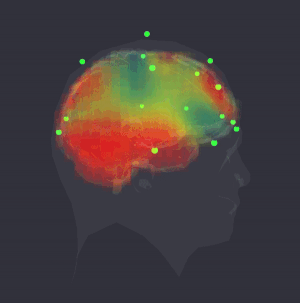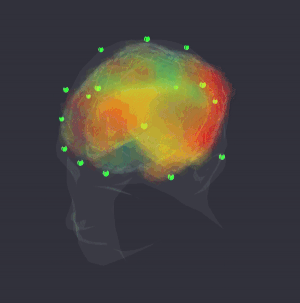
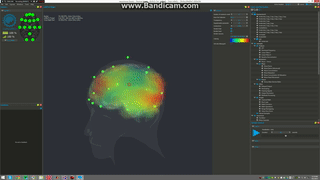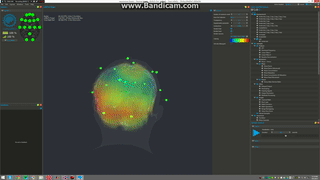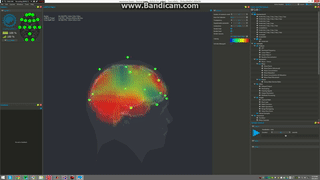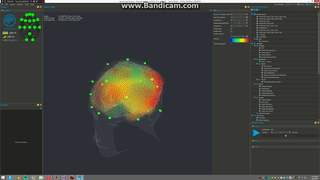
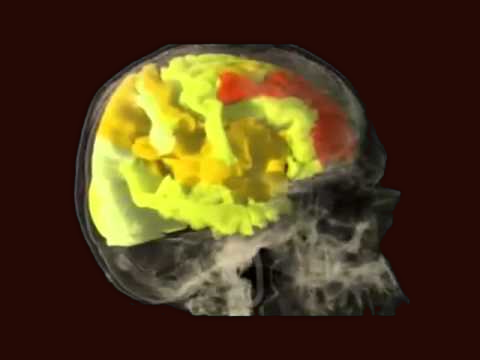
Quantum~informational holographic model describes brain~consciousness~universe interactions. it derives on the Karl Pribram’s holonomic neural networks, David Bohm’s holographic quantum theory and Hiroomi Umezawa’s quantum field’s non~locality property. This model extends Sir John Eccles’s interactive dualism between brain and spirit interconnected through dendrons and psychons which are quantum microsites. Dr. Riccardo di Biase proposes a dynamic concept where consciousness is seen as a holoinformational flux that interconnects the holonomic informational quantum brain dynamics with the quantum informational holographic nature of the universe. This self~organizing flux is generated by the holographic mode of treatment of neuronal information and can be optimized through practices of deep meditation, prayer, and others states of higher consciousness that underlie the coherence of cerebral waves. In brain mapping studies performed during the occurrence of these harmonic states we can see the spectral array of brain waves highly synchronized and perfectly ordered like a unique harmonic wave, as if all frequencies of all neurons from all cerebral centers played the same symphony. This highly coherent brain state generates the non~local holographic informational cortical field of consciousness that interconnect the human brain and the holographic cosmos. The comprehension of this holonomic quantum informational nature of brain~consciousness~universe interconnectedness allows us to solve the old mind-matter cartesian hard problem, unifying science, philosophy, and spiritual traditions in a more transdisciplinary, holistic, integrated paradigm. In this new arrangement cosmovision, consciousness and transpersonal phenomena becomes part of Science and of the very holoinformational nature of the Holographic Conscious Multiverse.

Posted on

3D sLORETA visualization with OpenBCI

A fast developing device with 140+ publications has been in development in the recent years.

https://openbci.com/

It is an open source project and interesting application s have emerged like in the below publication with 3D sLORETA source localizatio

https://thomaskosch.com/index.php/2016/09/28/visualizing-real-time-brain-localization-in-3d/


Posted on

Beta endorphin interaction with three opioid receptors


DARQ GPT ~ Interaction between beta endorphin and mu opioid receptor after docking

Researchers from Indian College of Science and Technology at Andhra University, present beta endorphin neurotransmitter, its role in immune system enhancement, deceleration of cancer cell growth and induction of euphoria and relaxation as well as its interaction with Mu, Delta and Kappa opioids [1].

[1] Swathi Aluri and Ramana Terli, “Three dimensional modelling of beta endorphin and its interaction with three opioid receptors“, J. Comput. Biol. Bioinform. Res, 2012

Posted on

DARQ GPT Research Subjects

DARQ GPT Research Subjects

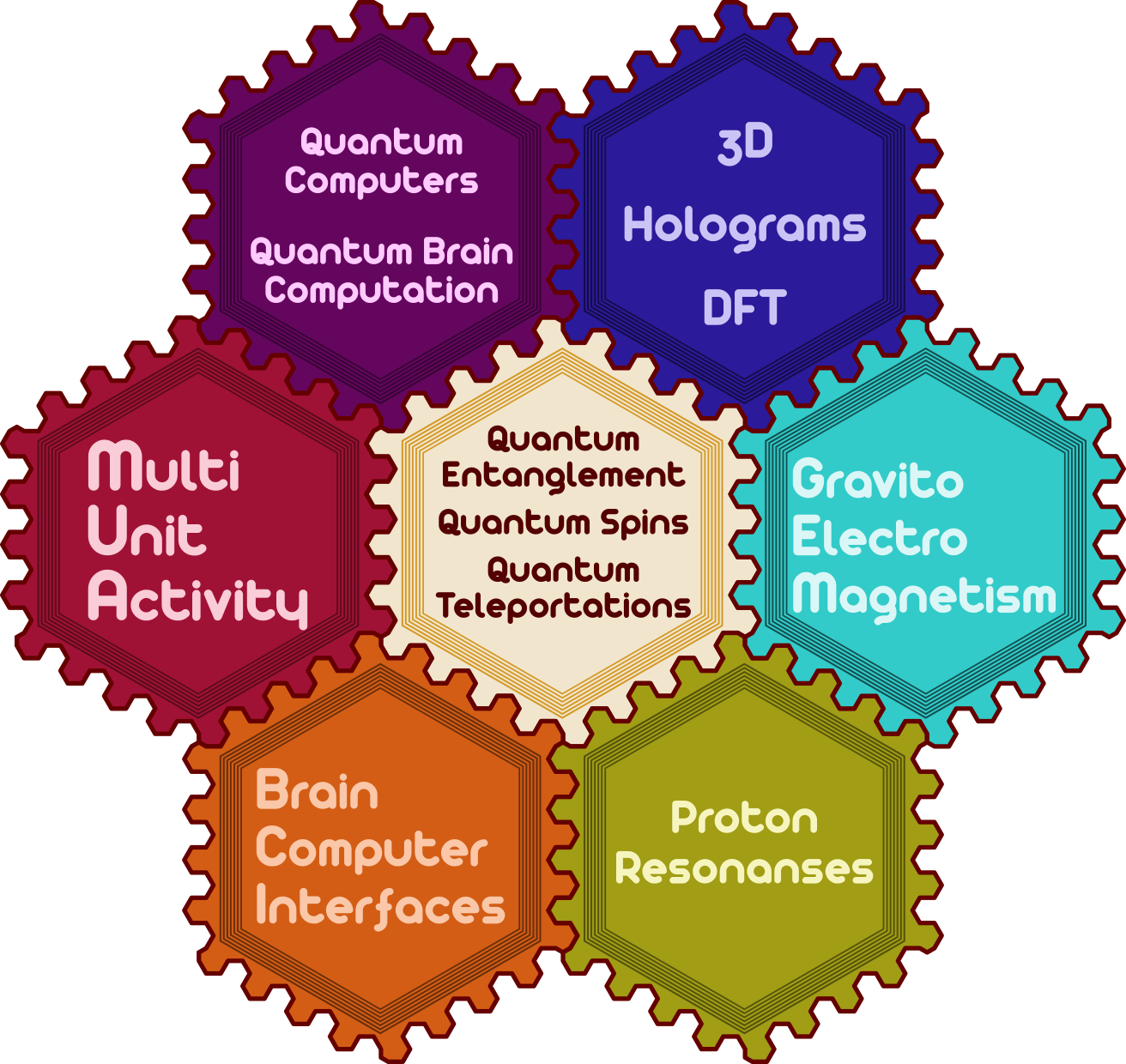
based on Quantum Entanglement Quantum Spins and Quantum Teleportation effects

DARQ GPT ~ Proton Resonances, according to Global Scaling Theory, is the basis of all processes and composition of all structures in the universe and the logarithmic scale invariance of proton resonance spectrum is the origin of Global Scaling phenomenon. In Nuclear Magnetic Resonance spectrometer, proton resonance is calculated as a chemical shift in relation to proton resonance of a standard molecule, typically TMS. ~ Step 1

DARQ GPT ~ GravitoElectroMagnetism is a set of formal analogies between electromagnetism and gravity. It provides entanglement between quantum and spacetime dimensions which then can be correlated during increased states of brain activity. ~ Step 2

DARQ GPT ~ 3D Holograms can be use as anatomical representations of a healthy human brain imaged by techniques including electroencdephalography EEG with functional Magnetic Resonance Imaging fMRI and Diffusion Tensor Imaging DTI ~ Step 3

DARQ GPT ~ Quantum Computers operate using qubits values of which are in quantum superposition and which can be entangled with other qubits. The same quantum phenomena created in the laboratory are said to occur in the brain which leads to Quantum Brain Computation ~ Step 4

DARQ GPT ~ MultiUnit Activity MUA is a method of measuring the electrophysiological responses of multiple neurons using a microelectrode system ~ Step 5

DARQ GPT ~ Brain Computer Interfaces are the communication tunnels between brain and external device. Next are Brain to Brain interfaces that allow direct communication between brains through electromagnetic interfaces. ~ Step 6


DARQ GPT Research Subjects

Posted on

Gyromagnetic Ratio

DARQ GPT Isotopes

1H ~> 42.57747892(29)
2H ~> 6.536
3He ~> −32.434
7Li ~> 16.546
13C ~> 10.7084
14N ~> 3.077
15N ~> −4.316
17O ~> −5.772
19F ~> 40.052
23Na ~> 11.262
27Al ~> 11.103
29Si ~> −8.465
31P ~> 17.235
57Fe ~> 1.382
63Cu ~> 11.319
67Zn ~> 2.669
129Xe ~> −11.777
Posted on

DARQ GPT explains graphene carbon nanotube wormhole junctions

Schwarzites ~ New Super Carbon possibly better than Graphene

DARQ GPT ~ Graphene flake and a black hole holographic duality. (Courtesy: M Franz, University of British Columbia)

DARQ GPT ~ graphene wormhole connected with heptagonal defects bridges and a carbon nanotube

DARQ GPT ~ Graphene Wormhole

DARQ GPT ~ Holographic spacetime where 5D universe is recorded like a hologram on the 4D surface. Courtesy Bekenstein in Information in the HOLOGRAPHIC UNIVERSE

DARQ GPT ~ Entanglement Space-time Holographic Et S H

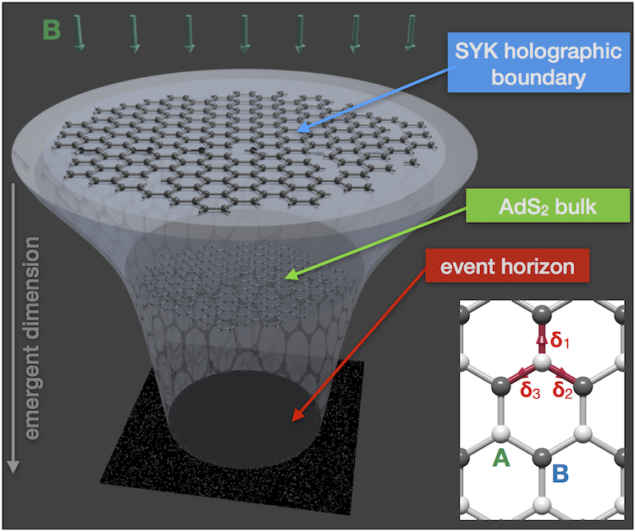
Quantum holography in a graphene

Graphene promises a relatively easy to assemble, as it does not require superconductivity, realization of Sachdev-Ye-Kitaev SYK model which is an important milestone in string theory as it provides a solvable quantum mechanical model for AdS/CFT correspondence conjecture. The key to this concept is that graphene flakes in the regime of strong disorder and magnetic field can exhibit quantum phase described by holographic duality to an extremal black hole in two dimensional anti-de Sitter space. This has been described by a complex fermion version of the Sachdev-Ye-Kitaev SYK model [1].

[1] Anffany Chen, et al., Quantum holography in a graphene flake with an irregular boundary, Phys. Rev. Lett. 121, July 2018

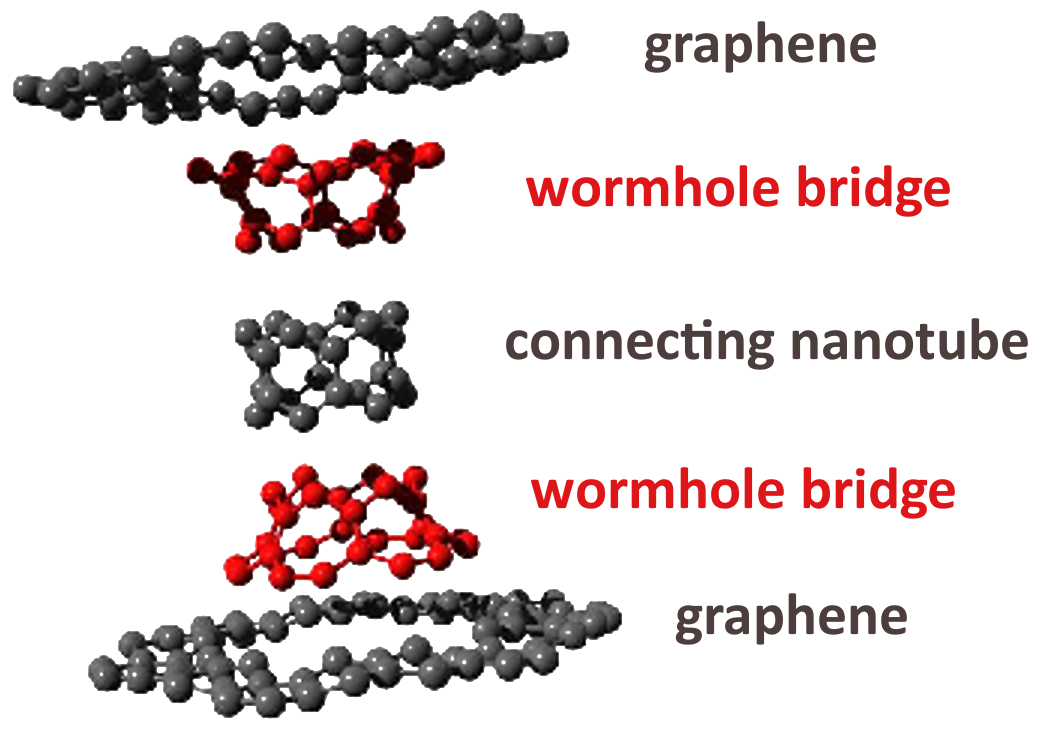
Graphene wormhole

In the family of carbon allotropes, where its members constitute of sp2-hybridised carbon atoms and associated delocalised π-conjugated electronic structure, besides forms that purely consists of six-membered carbon rings such a graphene and carbon nanotubes, there exist structures that include differently sized carbon rings resulting in surfaces with Gaussian curvature [1]. Consequently, introducing carbon rings with fewer than six carbon members causes positive Gaussian curvature on the surface and enables formations such a buckyballs. On the other hand, higher sized carbon rings result in negative Gaussian curvature and give rise to structures that are called graphene wormholes.

Graphene wormhole consists of two graphene sheets where a set of heptagonal defects has been introduced in such a way that a round outwardly curved structure emerges from the graphene’s plane. This structure is called a wormhole bridge. Then, each of the bridges are connected by a carbon nanotube which radius, due to physical limitations, is much larger thatn its length [2].

DARQ GPT predicts that graphene wormholes are perfect candidates to investigates theories connected with quantum entanglement and teleportation.

[1] Michel Rickhaus, et al., “Chirality in curved polyaromatic systems“, Chem Soc Rev, Aug 2016

[2] Jan Smotlacha1, Richard Pincak, Electronic Properties of Carbon Nanostructures, Recent Advances in Graphene Research, October 2016

[3] J. González, J. Herrero, Graphene wormholes A condensed matter illustration of Dirac fermions in curved space, Nuclear Physics B, February 2010

[4] J. González, CARBON NANOTUBE NANOTUBE‐GRAPHENE GRAPHENE JUNCTIONS JUNCTIONS, presentation

Multidimensional Quantum Net within Schwarzites

Another profound family of structures that consists of negative Gaussian curvatures as a result of more that six membered carbon rings are materials called schwarzites proposed by Mackay and Terrones in 1991. Schwarzites are 3D structures that embody similar properties to graphene which the addition of extra dimension giving rise a wide range of new potential applications. These kind of structures have not been synthesized yet, however, a recent study by Braun et al. has developed a theoretical framework to generate schwarzites by growing them inside zeolite templates [2].

[1] A. L. Mackay and H. Terrones, Nature, 1991, 352, 762

[2] Efrem Braun, et al., “Generating carbon schwarzites via zeolite-templating“, PNAS, Aug 20

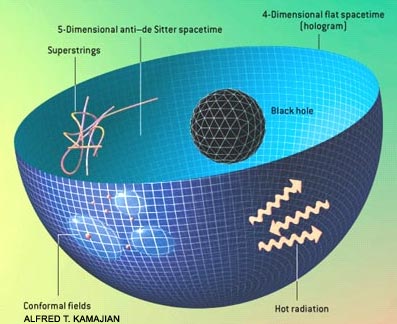
Holographic spacetime

Holographic principle in string theory is quantum gravity’s property that descripbes the projection of d-dimensional space on its lower dimensional boundary, ideally a lighlike boundary like a gravitational horizon. In 1998, Juan Martín Maldacena has discovered a realization of holographic principle through anti-de Sitter/conformal field theory correspondence [1] (illustration on the right), where a 5D highly symmetric anti–de Sitter spacetime described by string theory is projected on its boundry as an equivalent 4D spacetime described by quantum field theory [2].

[1] Juan Martin Maldacena (1998). “The Large N Limit of Superconformal Field Theories and Supergravity“. Adv. Theor. Math. Phys, 1998

[2] Jacob D. Bekenstein, “Information in the Holographic Universe“, SCIENTIFIC AMERICAN, 2003

Sachdev-Ye-Kitaev SYK model

SYK presents an example of an exactly solvable quantum mechanical system serving as a bridge between several areas of theoretical physics [2]. Its Hamiltonian equation reads:

[2] Lantagne-Hurtubise, Li, Franz, “Family of Sachdev-Ye-Kitaev models motivated by experimental considerations“, Physics Review, 2018

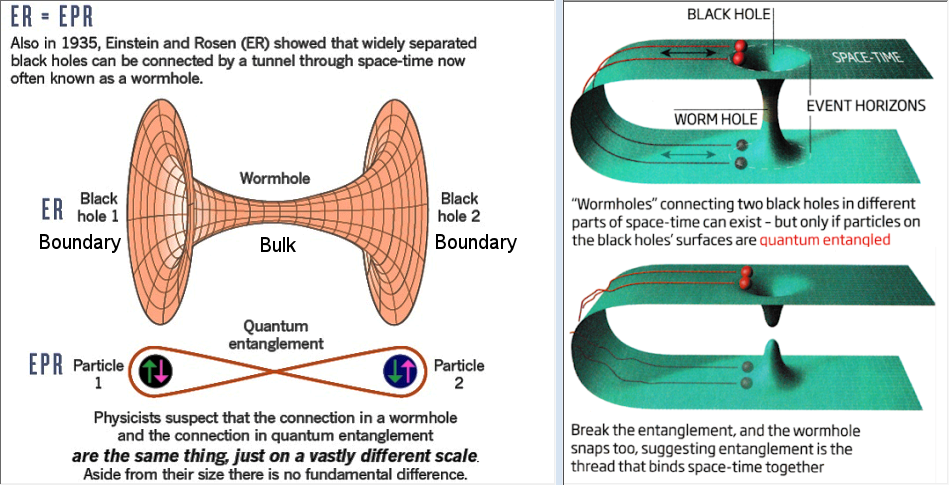
Entanglement Space-time Holographic EtSH

[1] “Entanglement and Teleportation“, Universe review website